Eindige Elementen Software

Algemeen

Om 3D rekensoftware goed te kunnen gebruiken is het belangrijk om een aantal zaken goed te begrijpen. In dit artikel leggen wij u een aantal zaken uit, zoals: wat is een lineaire berekening? Welke elementen toe te passen? Wat moet u weten over niet-lineaire berekeningen? Wat is belangrijkrijk bij de stabiliteitsberekening?

De meeste rekensoftware zijn 2D of 3D rekensoftware. 2D rekensoftware is bijvoorbeeld een raamwerkprogramma met een X en Z-as, waarbij portalen worden gecontroleerd. 2D rekensoftware is bijvoorbeeld ook een balkrooster programma of een ligger op meerdere steunpunten. In sommige gevallen is 2D software ook een platenprogramma waarbij vloeren worden gecontroleerd. 3D rekensoftware rekent gehele constructies uit in drie dimensies: X, Y en Z. Het voordeel van 3D rekenen is de koppeling met BIM-software, zoals Tekla(c) en REVIT(c) en de mogelijkheid om veranderingen snel door te voeren. Sommige constructeurs ervaren 3D rekenen als lastiger.

Eindige Elementen Types

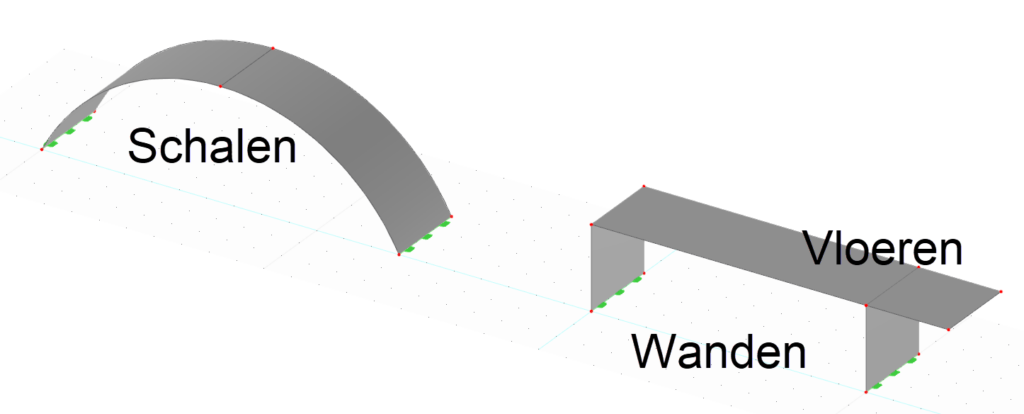
In RFEM worden er meerdere types eindige elementen toegepast. Zo worden Staven (1D), Wanden (2D), Vloeren (2D), Schalen (2D) en Volumes toegepast. 2D elementen hebben de eigenschap dat de constructeur de dikte ingeeft. Schalen zijn een combinatie van wanden en vloeren. Schalen kunnen zowel vlak als gekromd zijn. Volumes of Solids worden meestal gebruikt voor details van berekening of bij geotechniek als de vervorming in de Z-richting van een element belangrijk is.

Berekening

Berekening in Rekensoftware

Extra belangrijk om te onthouden is bij eindige elementen programma’s, zoals RFEM en RSTAB:

Belasten = Vervormen

De vervorming controleren is de eerste stap die een constructeur dient te doen bij het controleren van eindige elementen programma’s. Kloppen de vervormingen ten gevolge van het eigen gewicht en veranderlijke belasting? Zo ja, controleer dan de vervorming van de belastingcombinaties. Controleer dan pas de reactiekrachten en de snedekrachten. Bent u helemaal okay met de optredende vervormingen en krachten? Dan pas kunt u een spanningsberekening of Normcontrole uitvoeren.

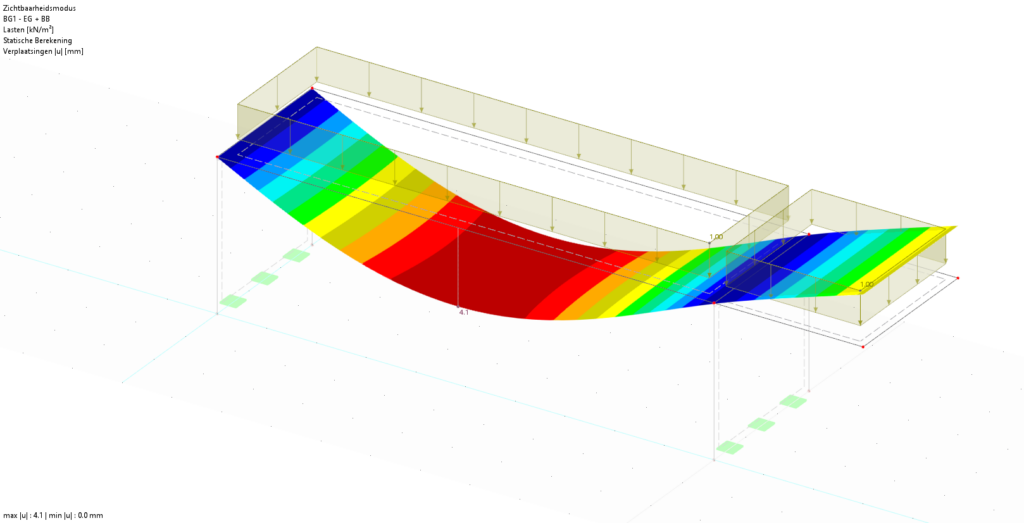
In 3D programma’s bijpaalt de berekening de volgende snedekrachten: Normaalkracht, de twee Dwarskrachten, de twee Buigende Momenten en het Torsiemoment. RFEM kan in sommige gevallen ook de Welving bepalen (7e vrijheidsgraad) indien dit bij dunwandige doorsnedes nodig is voor de juiste berekening van de stabiliteit.

Lineaire Berekening

De volgende relaties, de zogenaame constitutieve vergelijkingen, geven de relatie tussen de snedekrachten en de vervormingen aan:

• Normaalkracht N = E × A × epsilon(rek)
• Dwarskracht V(z/y) = G × A(z/y) × gamma(afschuifvervorming)
• Buigend Moment M(y/z) = E × I(y/z) × kappa(kromming)
• Torsiemoment T = G × Iw × rho(hoekverdraaiing)

De bovenstaande relaties zijn allemaal een variant van de wet van Hooke. Er is een linear verband tussen de snedekracht en vervorming. Om deze reden spreekt men van een Lineaire Berekening. De stijfheid is de vermenigvuldigsfactor waarmee verhouding bepaalt wordt. De stijfheid bestaat uit een materiaal gedeelte: de elasticiteitsmodulus of de glijdingsmodulus en uit een geometrisch gedeelte afhankelijk van de geometrie van de doorsnede of dikte van het beschouwde onderdel in een 2D element, zoals een vloer.

Immers geldt voor de normaalkracht en buigend moment: Moment / Traagheidsmoment = Elasticiteitsmodulus / Straal = Spanning / afstand tot uiterste vezel. (nb. Straal = 1 / kromming)

Bij staven kunnen de volgende snedekrachten optreden:

• N, Vy, Vz, Mx, My, Mz

Bij Wanden kunnen de volgende snedekrachten optreden:

• nx, ny, nxy

Voor vloeren kunnen de volgende snedekrachten optreden:

• vy, vz, mxy, mxx, myy

Bij schalen kunnen de volgende snedekrachten optreden:

• nx, ny, nxy, vy, vz, mxy, mxx en myy

2D Elementen

In dit artikel gaan we niet verder in op staafelementen of volume elementen. Wij behandelen enkel nog 2D elementen.

Bij een 2D eindig element is het belangrijk om op de volgende zaken te letten: de grootte van het element, de vorm van het element en de resultaten van het element. De grootte van een element is meestal 1 a 2 maal de dikte. Voor beton is meestal 2 maal de dikte voldoende. Voor staal elementen adviseren wij 1 maal de plaatdikte. Er zijn drie vormen van elementen: de driehoek, de rechthoek en vierkant. Het is belangrijk om te streven naar vierkantige elementen. Voor een theoretische achtergrond met betrekking tot eindige elementen en met betrekking tot de buigtheorie zoals Kirchhoff of Mindlin, adviseren wij bijvoorbeeld het boek van prof. Barth: “Finite Elemente in der Baustatik-Praxis”, Hoofduitgeverij Beuth Verlag.

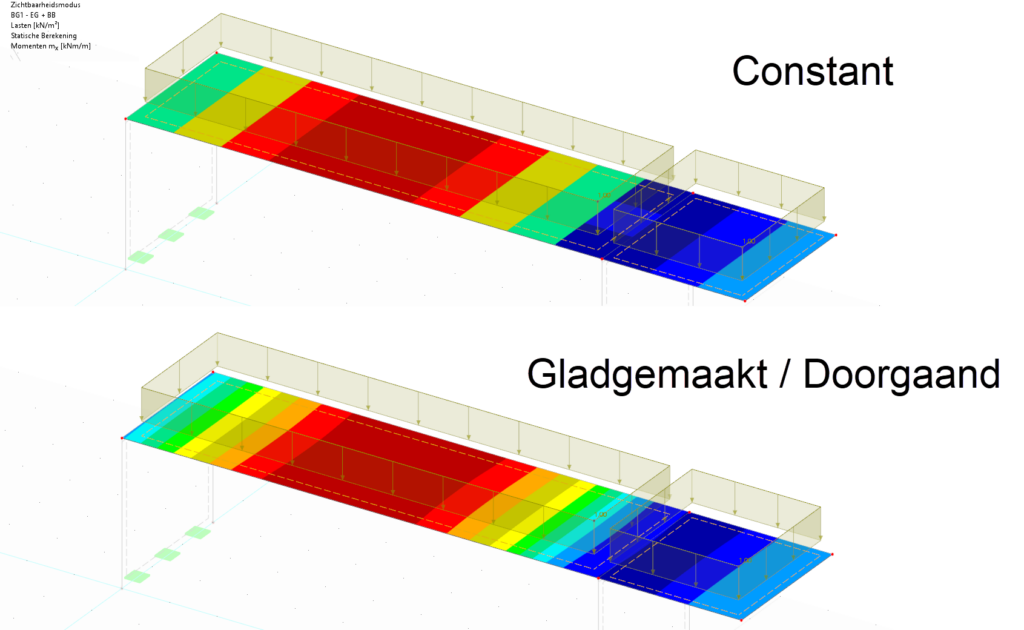
De resultaten van 2D elementen zijn de vervormingen en krachten, zoals reactiekrachten en snedekrachten. Omdat de vervorming door de Solver bepaald word in het zwaartepunt van een eindig element is het verstandig om voor de Staalberekening de resultaten als ‘Constant’ op het element te tonen. Indien de grootte van het element voldoende fijnmazig is, dan zijn de resultaten over het algemeen goed te gebruiken. Voor betonconstructies met een elementgrootte van twee maal de dikte kan de constructeur de ‘Gemiddelde’ functie gebruiken om resultaten te bekijken.

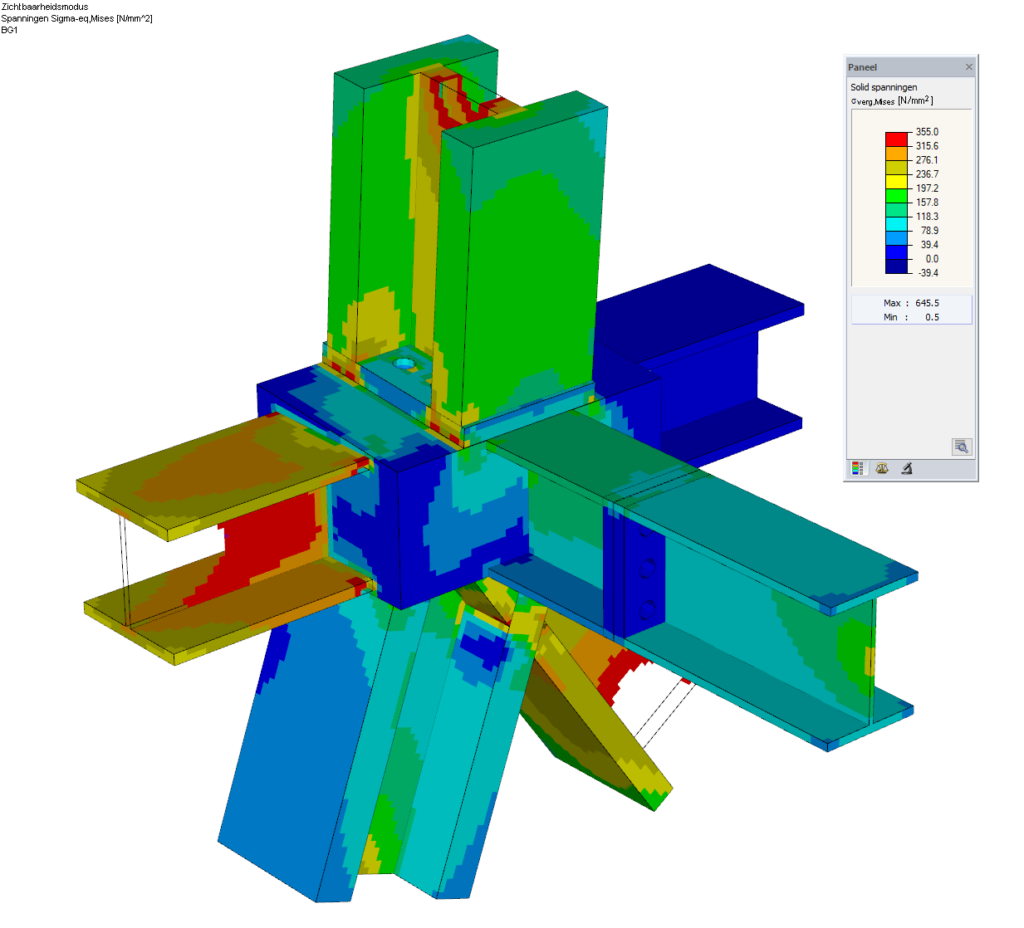
Bij het bespreiden van zogenaamde piekspanningen kun je als constructeur meerdere zaken doen: 1) Een realistische grootte van het eindige element toepassen en in de berekening de equivalente (piek)spanning verklaren, 2) Een zogenaamde middelingsgebied toepassen met voldoende eindige elementen. De waardes van de eindige elementen worden dan gemiddeld, 3) Een fysisch niet-lineare berekening doen, waarbij er wordt toegestaan dat het materiaal vloeit.

Niet-lineaire Berekening

Er zijn drie soorten niet-lineariteiten in RFEM: Type Niet-Lineairiteit, Geometrisch Niet-Lineairiteit en Fysisch Niet-Lineairiteit. In alle drie de gevallen is de berekening een niet-lineaire berekening. Dit betekent dat de berekening wordt uitgevoerd in een aantal iteratieve stappen totdat er aan het convergentie criterium is voldaan. De niet-lineaire berekening is niet anders dan een aantal lineaire berekeningen met steeds andere stijfheden. Voor niet-lineaire berekening geldt dat resultaten van diverse belastinggevallen en/of -combinaties niet bij elkaar mogen worden opgeteld. Er is geen sprake van zogenaamde super positie.

Type Niet-Lineair

Type Niet-Lineair is bijvoorbeeld een enkel druk steunpunt, een wrijvingsveer, contactvlak, zoals een kopplaat, kabel, tentdoek of een windverband dat enkel trek kan opnemen. Deze niet-lineairiteiten worden per object ingesteld. Zo is een windverband een staaf van het type ‘TREK’.

Geometrisch Niet-Lineair

Er zijn drie geometrisch niet-lineaire berekeningen: 2e orde ofwel P-Delta, Grote Verplaatsingen (kabels), en Nakritisch. Bij 2e orde berekening gaat de berekening uit van kleine verplaatsingen, sin phi = phi. Deze berekening komt veel voor bij staaf en wand constructies. Ten gevolge van de normaalkracht treedt er geen dwarskracht op. Bij de grote verplaatsingen is dit wel zo. Deze berekening is noodzakelijk bij kabel, en membraanberekeningen. Bij Nakritisch kan de berekening het post-knik gedrag van bijvoorbeeld een kolom berekeken. Dit wordt in de praktijk echter weinig gebruikt.

Fysisch Niet-Lineair

Bij een fysisch niet-lineaire berekening wordt er rekening gehouden met het elasto-plastische en plastische gedrag. Meestal is het gedrag ideaal plastisch; dit betekent dat er na het bereiken van de vloeispanning enkel de rek nog kan toen nemen, de kracht/spanning blijft gelijk. In 2D elementen houdt RFEM via de addon Nonlinear Material Behaviour rekening met het plastische gedrag. De constructeur dient een relevant materiaal model te kiezen. Voor betonberekeningen zoals in de addon Concrete Design bepaalt RFEM op basis van spanning/rek diagrammen van beton en wapening het evenwicht in de doorsnede en 2D elementen. De vervormingen houden hierdoor rekening met het scheurgedrag van beton.